Linear correlator
A linear correlator is a digital correlator with a linear spacing in the channel layout. It finds applications for DLS, DWS, FCS, and other light scattering technologies. All these techniques require the unnormalized photon rate autocorrelation function, which in a first approximation reads:
where the time axis has been discretized over samples and
is the time lag between the photon count rates
and
. Computation of the previous quantity can be carried out through a digital correlator, whose simplest schematic is shown in the figure below. The basic operations performed by a digital correlator for
samples are:
- Count photoelectron pulses upon a sampling time Δt.
- For each correlation channel k, delay the samples by Δt, such that
.
- For each channel, multiply the delayed samples by the current one.
- For each channel, sum the products.
This scheme, known as the linear correlation scheme, is characterized by a subsequent set of equally spaced time operations for a fixed sampling time Δt. The extension of the lag time range is evidently determined by the maximum number of channels available. The main limitation of this system lies in the finite implementable number of channels. In fact, to obtain high measurement accuracy, a very short sampling time, usually of the order of 10 ns is required. Under these constraints, a total measurement duration of even 1 s would require a dynamic range of 108 s and a corresponding number of channels of 108, which is technically unfeasible.
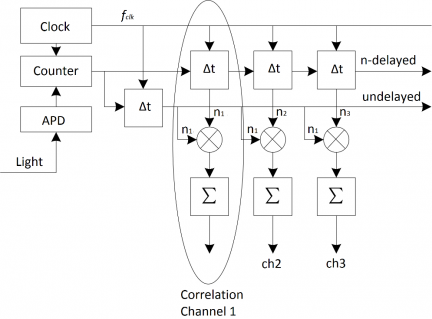
Linear correlator architecture
In addition, the inherent discretization of the time axis, and the resulting averaging of the photoelectron signal, sampled over Δt, yields distortions of a decaying correlation function, increasingly evident when the lag time is considerably larger than Δt. For normalization of the numerical correlation function please check the mutli-τ correlator page.
