LS Instruments | Characterization of Dilute and Concentrated PNiPAM-BiS Microgel Suspensions

Characterization of Dilute and Concentrated PNiPAM-BiS Microgel Suspensions

Application Note_Characterization of Dilute and Concentrated PNiPAM-BiS Microgel Suspensions.pdf

LS Spectrometer™ II

The LS Spectrometer^TM II is a goniometer-based variable-angle light scattering instrument for static- (SLS) and dynamic light scattering (DLS). The LS Spectrometer^TM II allows for the most comprehensive nanoparticle characterization and can be further upgraded with various options, such as Modulated 3D technology for the measurement of turbid samples.

See Details

Introduction

We have employed a 3D dynamic light scattering (DLS) scattering instrument to study both dilute and concentrated, aqueous suspensions of Poly-(N-isopropyl-acrylamide) (PNIPAM) microgel particles cross-linked with N, N-methylenbisacrylamide (BiS). Static and dynamic light scattering experiments with dilute samples at different temperatures reveal the thermal response of these microgel particles, which does well with increasing temperature. For concentrated suspensions at volume fractions θ ~ 0.5, we find intensity correlation functions displaying a two-step decay. The mean squared displacements found by transforming the correlation function at scattering wave vectors, q, close to the structure peak reflect confined particle dynamics at short lag-times and cage escape dynamics at large enough lag-times. The static light scattering (SLS) data exhibits an unusual rise at low q, suggesting possible formation of structures larger than the length scale defined by a single particle diameter.

SLS and DLS of dilute PNiPAM-BiS microgel suspensions

We have characterized our PNiPAM-BiS microgel particles using SLS and DLS for temperatures within the range 10°C ≤ T ≤ 40°C. In all SLS experiments and at large enough q-vectors, the scattered intensity depends linearly with q²when displayed in a logarithmic-linear scale; this indicates that in the available q-range of our experiments we access the Guinier region of the microgel form factor, as shown in Figure 1a [1]. Furthermore, the slope of the scattered intensity increases when the temperature is increased, indicating the decrease in the particle size. Since our suspensions are dilute, there are no spatial correlations between the particles and beside prefactors, the scattered intensity I(q) corresponds to the microgel form factor, P(q). In the Guinier region, P(q) ~ exp(-R_g²q²/3) [2] and therefore from a plot of log I(q) versus q², it is straightforward to obtain the radius of gyration, R_g, for every temperature, which is shown in Figure 1c with open circles.

We can also quantify this de-swelling behavior using DLS. We measure the intensity correlation functions, $g_2(\tau) - 1$ , and find they exhibit a linear dependence with the lag time $\tau$ , when displayed in a logarithmic-linear scale. This indicates the exponential character of these functions, as shown in Figure 1b. Since the scattered intensity fluctuations are Gaussian, the Siegert relation must be fulfilled:

$g_2(\tau)-1=g_1(\tau)^2$ ,

where $g_1(\tau)$ is the field correlation function [3]. Furthermore, since the suspension is dilute, we expect no correlations between particles and thus $g_1(\tau)$ must reflect the diffusion of the particles. In this case, $g_2(\tau)-1\sim {\rm exp}({-2\tau / \tau _0)$ , where $\tau_0=1/(q^2D)$ , with D the diffusion coefficient [4]. We further confirm that the dynamics are diffusive by verifying that $\tau_0$ depends linearly on q², and use the slope of the corresponding linear fits to determine D at different temperatures. We relate D to the hydrodynamic radius of the particles, R_h, invoking the Stokes-Einstein relation:

$D=\frac{k_BT}{6\pi\eta R_h}$ ,

with k_Bthe Boltzmann constant, T the temperature and η the solvent viscosity. Consistent with the findings for the radius of gyration, we find that R_hdecreases with temperature, as shown in Figure 1c with closed circles.

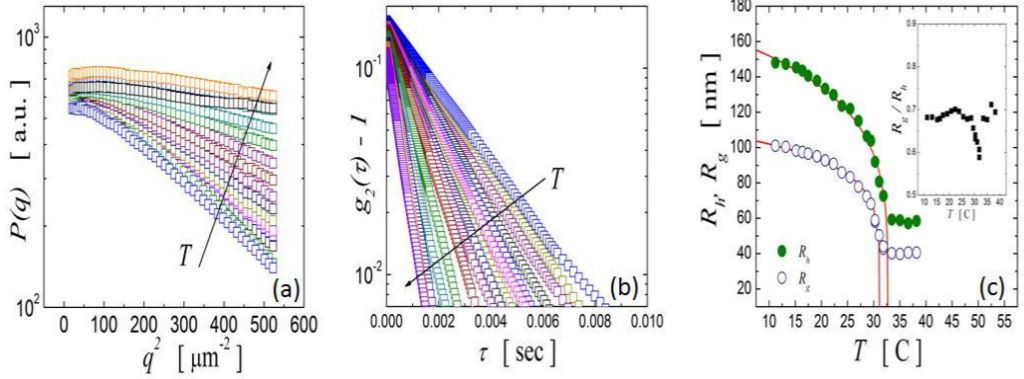
Figure 1. SLS (a) and DLS (b) profile of dilute PNIPAM-BiS microgel suspensions at temperatures ranged 10°C ≤ T ≤ 40°C. From SLS and DLS experimental datasets it is possible to obtain the temperature evolution of the hydrodynamic radii, R_h, and the radii of gyration, R_g(c). The inset displays the ratio R_h/R_gwhich states the soft character of these type of microgels.

Our results indicate that both radii progressively decrease with temperature until the lower critical solution temperature (LCST) of the polymer is reached. At this temperature, the particle size abruptly decreases down to a minimal size and does not vary for temperatures above the LCST. Note that above the LCST, the interaction between the particles contains an attractive contribution. However, we do not observe aggregation, indicating there must also be a repulsive contribution to the particle-particle interactions, which in our case results from the presence of charge at the surface of the particles from the ionic initiator used in the microgel synthesis [5]. This charge remains unscreened and provides suspension stability for T > LCST. Below the LCST the volume transition is well described by a functional form $R\sim A(1-\frac{T}{T_c})^\alpha$ for both R_hand R_g, with A the radius at zero temperature and T_ca critical temperature. We find T_c>>LCST and α=0.235 for R_hand α=0.167 for R_g, as shown in Table 1.

Despite the behavior of R_hand R_gwith temperature is remarkably similar, they have very different magnitudes; the hydrodynamic radius is larger than the radius of gyration at all temperatures. We find that the ratio R_g/R_his almost constant with temperature and equal to R_g/R_h~ 0.7, as shown in the inset of Figure 1(c). This value is smaller than that for hard spheres, where R_g/R_h~ 0.8 [1]; this reflects the uneven distribution of cross-linker, which decreases from the center of the particle towards its periphery [5]. We also note that our result is higher than the characteristic value obtained for other soft particles, R_g/R_h~ 0.6 [6].

Interestingly, near the LCST this ratio decreases down to ~0.58, emphasizing the peculiar properties of these particles around this temperature, which can lead to rich suspension behavior [7]. Note that the critical temperature corresponding to static measurements is slightly lower than the one found for dynamic measurements (Table 1), emphasizing the soft character of the particles near the LCST.

	A [nm]	T_c(C)	$\alpha$
DLS (R_h)	177	32.8	0.235
SLS (R_g)	112	31.1	0.167

Table 1: Respective fit parameters to the temperature evolution of the radii of gyration (denoted as SLS R_g) and the hydrodynamic radii (denoted as DLS R_h) to a critical-like functional form $R\sim A(1-\frac{T}{T_c})^\alpha$ .

SLS and DLS of concentrated PNiPAM-BiS microgel suspensions

Static and dynamic light scattering experiments were performed on PNiPAM-BiS microgel suspensions at a volume fraction F~ 0.5 and at a temperature T= 20°C. The system at this concentration is significantly turbid and the use of the cross-correlation schemes is required in order to extract single scattering information. In static experiments, multiple scattering is corrected by the intercept of the correlation function [8]:

$I(q)=[I_1(q)I_2(q) \beta_{12}/\beta_{1}]$ ^1/2, where I(q) is the time-averaged single scattered intensity, I₁(q )and I₂(q) are the time-averaged scattered intensities detected at each detector of the 3D instrument, $\beta_{12}$ is the intercept at the temperature, q-vector and incident light intensity of the experiment, and $\beta_{1}$ is the intercept measured at dilute conditions in the sole presence of single scattering. To obtain the effective structure factor, S_eff(q), we normalize the single scattered intensity I(q)by the intensity scattered by a dilute suspension of microgels, P(q), at the same experimental conditions, and correct for the concentration difference: S_eff(q)= I(q) c_dil/ (P(q) c_conc), where c_concand c_dilare the particle concentrations of the concentrated and dilute samples, respectively. Since the temperature and concentration variations of optical constants such as the refractive index of the microgel particle are not known, we measure an effective structure factor.

The effective structure factor is characterized by a strong increase at the largest q-vectors accessible with the 3D DLS instrument, as shown in Figure 2a. However, note that a structure peak does not appear in our measurement which for the case of hard spheres would be located at a position $q_{\rm peak}=\frac{\pi}{R_h}=0.024\,\, {\rm nm}^{-1}$ . By contrast, the continuous rise of S_eff(q) at q-vectors above the expected q_peaksuggests a relevant length scale that is smaller than the particle size. Note, however, then the particles are not hard spheres since R_g/R_his only equal to 0.7. In addition, the cross-linker concentration is higher at the center of the particle than it is at the particle periphery, possibly affecting the particle-particle interactions due to possible interpenetration and outside-polymer compression.

We also note that S_eff(q) exhibits a slight rise at low q. This feature is unusual [9] and suggests there could be large structural correlations in the sample or propensity of single microgel particles to form cluster-like structures. We also perform DLS experiments on this concentrated sample at $q=0.0237\,{\rm nm}^{-1}$ , which is located to the left of the structure factor peak and corresponds to a distance $\frac{2 \pi}{q}=266$ nm. This distance is of the order of the particle diameter and close to the mean separation between particles. As a result, the probed motion corresponds to single-particle dynamics.

The intensity correlation function exhibits a double decay, as shown in Figure 2b. Since $g_2(\tau )-1$ fully decays to zero, the system is ergodic and the time average dynamics from the scattering volume is representative of the ensemble average dynamics of the system.

Figure 2: SLS (a) and DLS (b) profile of PNIPAM-BiS microgel suspensions at a temperature T=20°C and θ~0.5. The dynamic measurement is at a q = 0.0237 nm^-1. The DLS correlation function g₂(τ)–1 is transformed into the particle mean squared displacement in (c).

Conclusion

To gain physical insight on the particle dynamics, we transform the correlation function into the particle mean squared displacement (MSD), $\left \langle \Delta r^2(\tau) \right \rangle$ , which we plot as a function of the lag time in Figure 2(c). Since the chosen q-vector nearly corresponds to the structure factor peak position, the msqd describes single-particle dynamics. It is characterized by sub-diffusive behavior at short lag times followed by a plateau reminiscent of kinetic arrest. However, for even larger lag times, the msqd increases with time again. The sub-diffusive behavior corresponds to $\left \langle \Delta r^2(\tau) \right \rangle\sim \tau^{0.62}$ , while the longtime behavior is consistent with $\left \langle \Delta r^2(\tau) \right \rangle\sim \tau$ , which corresponds to diffusion. The plateau in the MSD at intermediate times is typical of systems approaching a kinetically arrested state, such as supercooled liquids on the approach to the glass or a transient colloidal gel [10, 11]. We find a plateau value, δ²∼0.1 $R_h^2$ . The diffusive dynamics at long lag time dynamics result from particles escaping from the surrounding cage formed by their neighbors [12]. Finally, we note that the dynamic measurements were performed for 14 hours with the absence of significant aging. This could be interpreted as suggesting that within the length of the experiment, cage escape results from the break-up of the associative structures suggested by the low-q increase of the effective structure factor. However, more experiments are underway to fully explore the behavior of this soft-particle system.

References

[1]    Pusey P.N: Introduction to Scattering Experiments, in Neutrons, X-Rays and Light: Scattering Methods Applied to Soft Condensed Matter. 2002, Amsterdam: Elsevier p. 3-21.
[2]    A. Guinier and G. Fournet: Small-Angle Scattering of X-Rays. 1955, New York: Wiley Interscience.
[3]    P. N. Pusey: Dynamic Light Scattering, in Neutrons, X-Rays and Light: Scattering Methods Applied to Soft Condensed Matter. 2002, Amsterdam: Elsevier p. 203-220.
[4] B.J. Berne and R. Pecora: Dynamic Light Scattering. 1976, New York: Wiley
[5]    H. Senff and W. Richtering: Temperature sensitive microgel suspensions: Colloidal phase behavior and rheology of soft spheres. Journal of Chemical Physics, 1999. 111(4): p. 1705-1711.
[6]    A. Fernandez-Nieves, F.J. de las Nieves, A. Fernandez-Barbero: Static light Scattering from microgel particles: Model of variable dielectric permittivity. Journal of Chemical Physics, 2004, 120(1): p. 374-378.
[7]    G. Romeo, A. Fernandez-Nieves, H. W. Hyss, D. Acierno, D. A. Weitz: Temperature-Controlled Transitions Between Glass, Liquid, and Gel States in Dense p-NIPA Suspensions, Advanced Materials (accepted).
[8]    C. Urban and P. Schurtenberger: Characterization of Turbid Colloidal Suspensions Using Light Scattering Techniques Combined with Cross-Correlation Methods. Journal of Colloid and Interface Science, 1998, 207, p. 150-158
[9]    G. Nägele, O. Kellerbauer, R. Krause and R. Klein: Hydrodynamic effects in polydisperse-charged colloidal suspensions at short times. Physical Review E, 1993, 47, p. 2562-2574
[10] A.H. Krall and D.A. Weitz: Internal Dynamics and Elasticity of Fractal Colloidal Gels. Physical Review Letters, 1998. 80(4): p. 778-781.
[11] B. R. Dasgupta and D.A. Weitz: Microrheology of cross-linked polylamide networks. Physical Review E, 2005, 71, p. 021504 1-9
[12] W. van Megen and S.M. Underwood: Glass Transition in Colloidal Spheres: Mode-Coupling Theory Analysis. Physical Review Letters, 1993, 70(18), p. 2766-2768

Back to Applications Download as PDF