LS Instruments | Structure Factor

Structure Factor

The inter-particle interference is taken into account by the so-called structure factor, $S(q),$ which is defined as

$S(q,c) = \frac{1}{N} \sum_{j,k}^{ }\left \langle exp([-iq\cdot (r_j(t)-r_k(t))]) \right \rangle,$

here r_j(t) and r_k(t) are the positions at the time t of particles j and k, respectively, and angle brackets signify time averages. In the formula above the scalar product of the scattering vector times the particle distance represents the phase shift between the light scattered by particle j and k.

As in the case for the form factor, we can introduce a pair correlation function, g(r,c) and, accounting only for pair interactions, the formula above is simplified to

$s(q)=1+c\int_{0}^{\infty} [g(r,c)-1]\frac{sin(qr))}{qr}(4\pi r^2)dr,$

here the physics of the "pair level" interaction is contained in the pair correlation function, g(r,c) that once specified allows calculating the structure factor either analytically or numerically.
As an example, Fig. 1 shows the structure factor calculated from the Percus-Yevick hard-sphere correlation function. We see that for very small particle concentrations where particle interactions are negligible the structure factor is equal to 1, whereas as the particle concentration increases a destructive interference effect appears at small scattering vectors due to reduced probability to find particles in close contact.

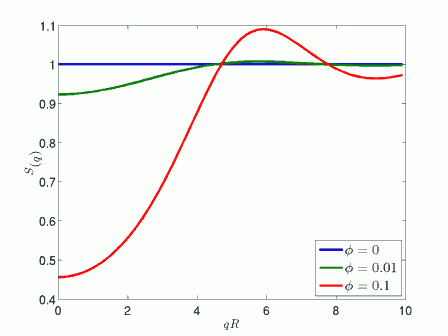
Figure 1: Hard Sphere Structure Factor at different volume fractions

As in the case of the form factor, an expansion for small q-values yields useful information. In the case of the structure factor about important thermodynamic properties of the colloidal suspension. Indeed it can be shown that

$\lim_{q \to 0} S(q,c) = \frac{N_A}{M}k T \left ( \frac{\partial \Pi}{\partial c}\right)^{-1}$

with $N_a$ the Avogadro's number, $M$ the molecular weight, $k$ Boltzmann constant, $T$ the system temperature, and $(\partial \Pi / \partial c)^{-1}$ the osmotic compressibility. Such a relationship becomes even more useful in the limit of small particle concentrations where the well-known virial expansions allow us to write

$\lim_{c,q \to 0} S(q,c) = 1 - 2 B_2 c,$

where B₂ is the second virial coefficient expressed in terms of particle number concentration.

Previous Chapter Next Chapter