LS Instruments | Form Factor

Form Factor

For homogeneous objects, the form factor is expressed as

$P(\mathbf{q}) = \left[\frac{\int_{V_p}dV\exp[-i\mathbf{q}\cdot\mathbf{r}]}{V_p}\right]^2$

For a sphere of radius $R$ the formula above evaluates to

$P(q) = \left[\frac{3}{(qR)^3}(\sin(qR)-qR\cos(qR))\right]^2$

Fig. 1 shows the form factor of a sphere according to the formula above. In agreement with what stated in the previous paragraph, we notice that for $q R \ll 1$ the form factor attains a plateau at a value of 1, whereas as soon as qR becomes substantially larger than 1 the form factor is affected by the interparticle interference effects.

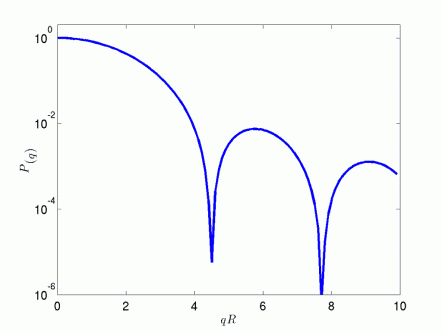
Figure 1: Sphere Form Factor.

A simpler general formula for the form factor can be obtained by introducing the so-called pair distance function, g(r) i.e. the probability to find two points belonging to the colloidal particle at a distance $r$ :

$P(q) = \left[\int_0^\infty r^2 g(r)\sin(qr)/(qr)dr\right]^2$

By expanding in series the term $sin(qr)/(qr)$ we obtain the Guinier approximation for the form factor:

$P(q) \simeq 1 - \frac{(q R_g)^2}{3},$

where the (optical) radius of gyration is defined as

$R_g^2 = \int_0^\infty r^2 g(r)dr.$

The importance of such approximation lies in the fact that it allows for the determination of a size parameter, namely $R_g$ by performing a simple linear fit in the plot $I_3$ vs. $q^2$ , the so-called Guinier plot. As an example, Fig. 3 shows the approximation for a sphere for which $R_g = \sqrt(3/5)R$ .

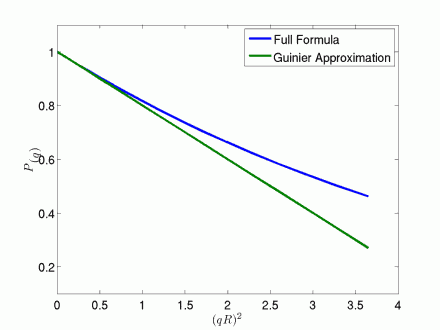
Figure 2: Sphere Form Factor, Guinier Plot.

Previous Chapter Next Chapter