Dynamic Light Scattering DLS
Dynamic Light Scattering (DLS, also known as Photon Correlation Spectroscopy or Quasi-Elastic Light Scattering) is one of the most popular light scattering techniques because it allows particle sizing down to 1 nm diameter. Typical applications are emulsions, micelles, polymers, proteins, nanoparticles, or colloids. The basic principle is simple: The sample is illuminated by a laser beam and the fluctuations of the scattered light are detected at a known scattering angle θ by a fast photon detector.
Simple DLS instruments that measure at a fixed angle can determine the mean particle size in a limited size range. More elaborated multi-angle instruments can determine the full particle size distribution.
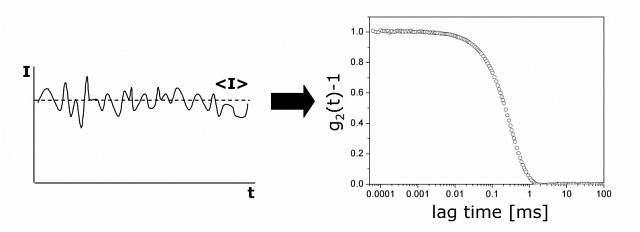
From a microscopic point of view, the particles scatter the light and thereby imprint information about their motion. Analysis of the fluctuation of the scattered light thus yields information about the particles. Experimentally one characterizes intensity fluctuations by computing the intensity correlation function g2(t), whose analysis provides the diffusion coefficient of the particles (also known as diffusion constant).
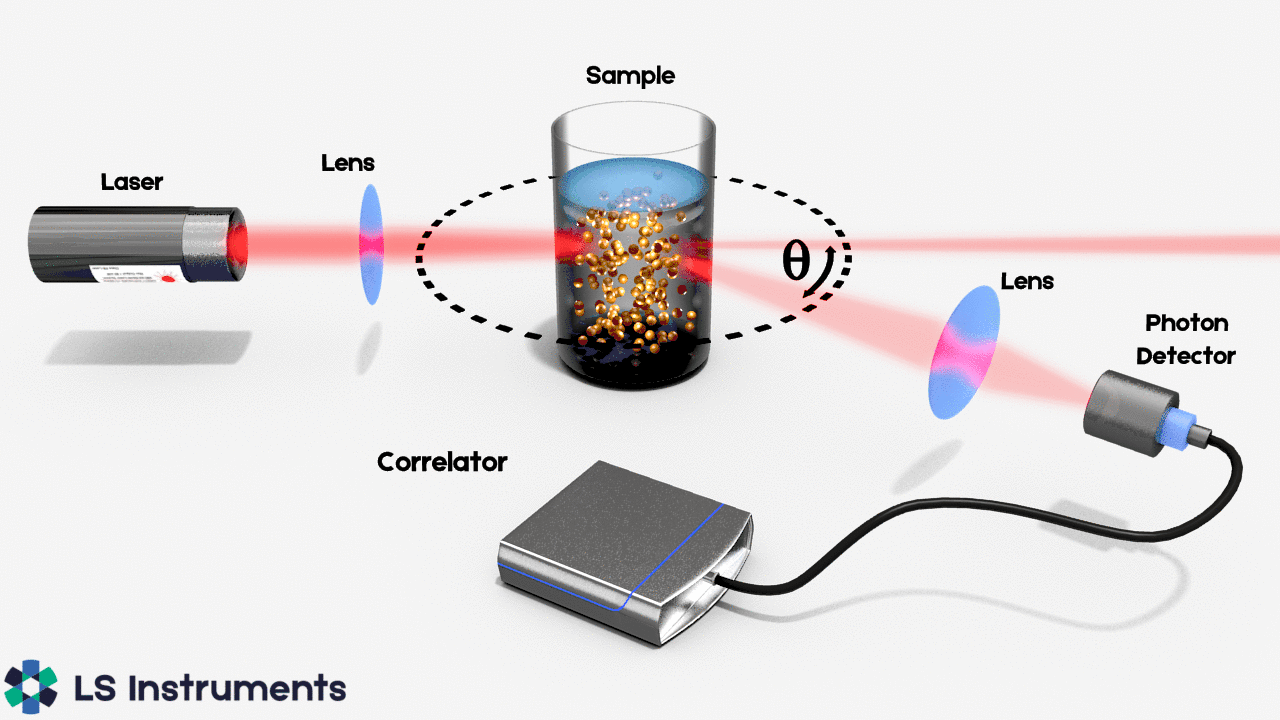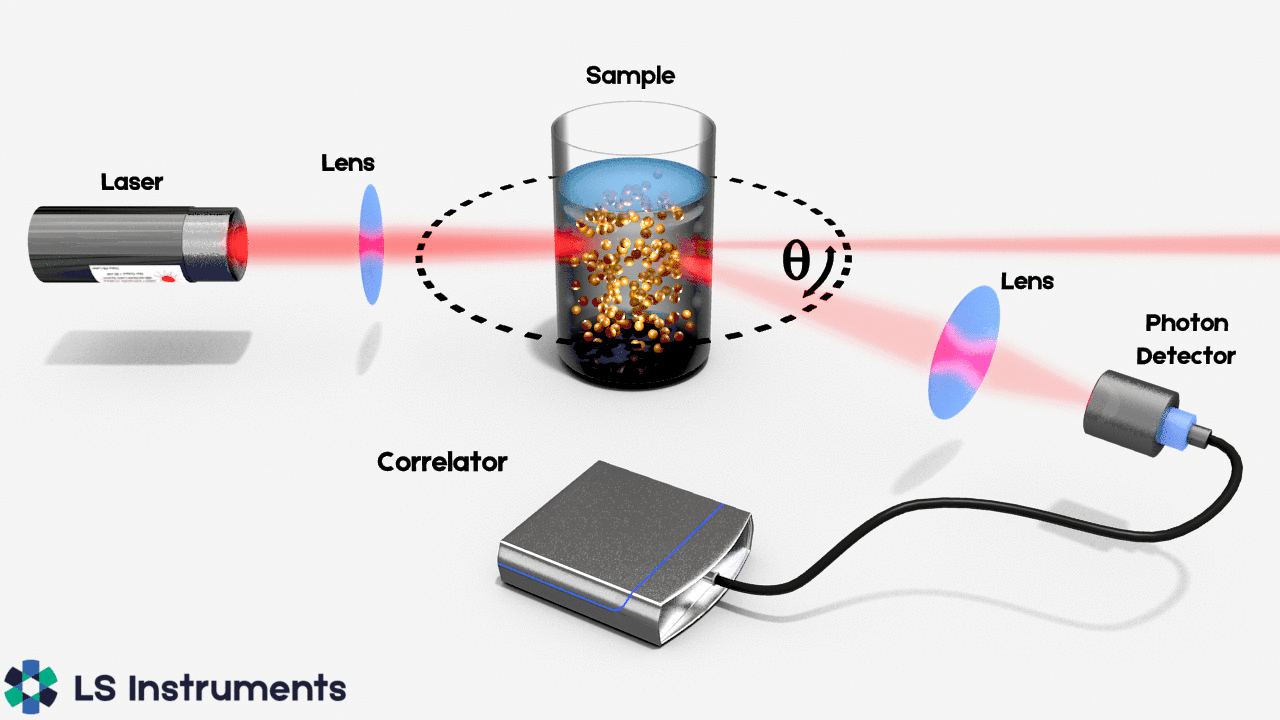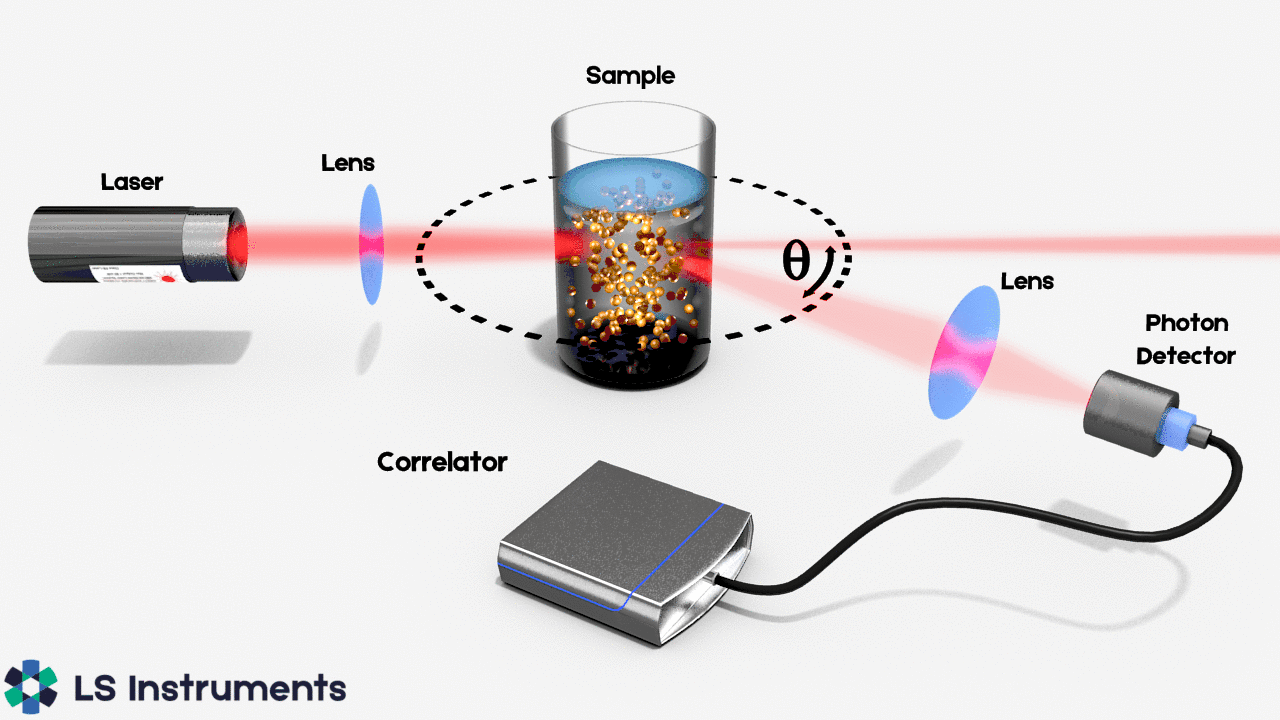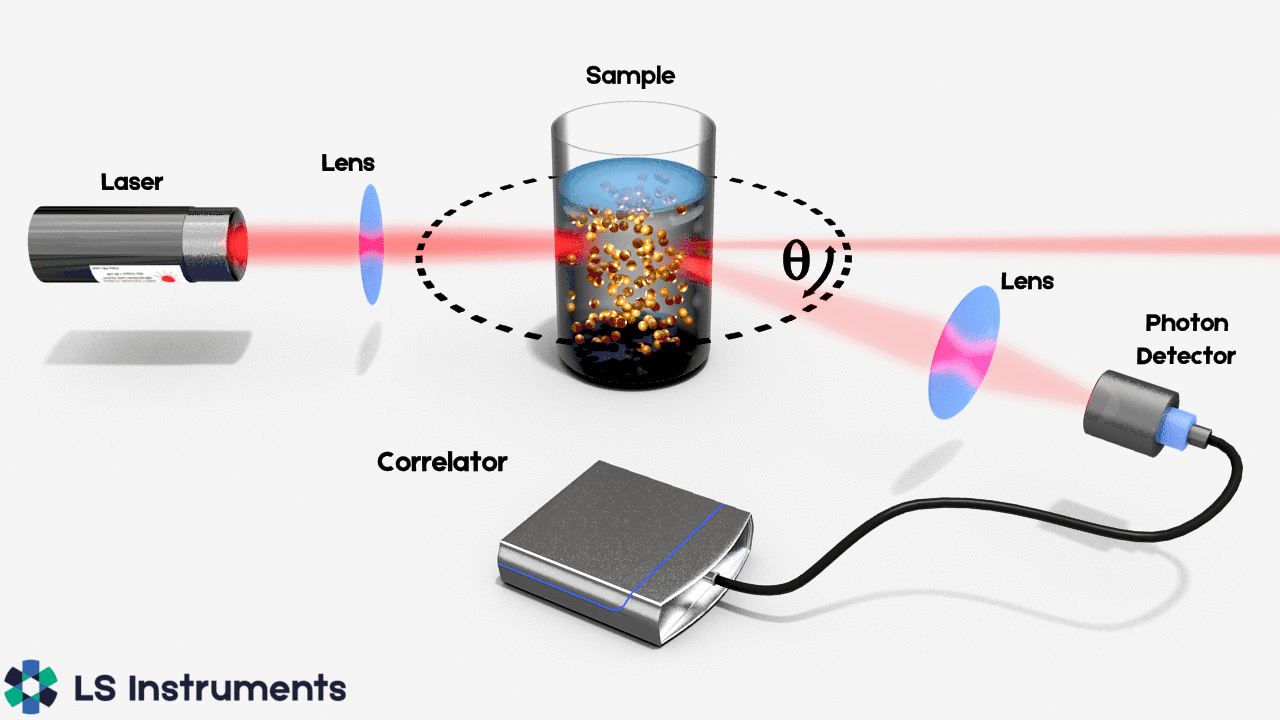
The diffusion coefficient D is then related to the radius R of the particles by means of the Stokes-Einstein Equation:
Where kB is the Boltzmann-Konstant, T the temperature, and η the viscosity.
The correlation of the intensity can be performed by electronic hardware (digital correlator) or software analysis of the photon statistics. Because fluctuation is typically in the range of nanoseconds to milliseconds, electronic hardware is typically faster and more reliable at this job. For more details on the theory of Dynamic Light Scattering please visit our DLS theory page.
Quality of Measurement
The quality of a DLS measurement depends on several factors. Some obvious, such as the quality of the components (the laser, the detector, the correlator...), other factors are not as straightforward but may influence the measurement significantly. Some important points to be considered are listed below.
The Scattering Angle
The decay rate depends on the wave vector and thus the scattering angle. Particles of different sizes scatter with different intensities depending on the scattering angle. Thus there is an optimum angle of detection for each particle size. A high-quality analysis should always be performed at several scattering angles (multiangle DLS). This becomes even more important in the case of polydisperse samples with unknown particle size distribution since, at certain angles, the scattering intensity of some particles will completely overwhelm the weak scattering signal of other particles, thus making them invisible to the data analysis at this angle.
DLS instruments working exclusively at a fixed angle can only deliver good results for some particles. Therefore, special attention should be paid while considering the precision of an advertised DLS instrument. For these fixed angle instruments, such indications are only ever true for certain particles.
Multiple Scattering
The theory of Dynamic Light Scattering is only valid for single scattered light. Like all scattering methods, the interpretation becomes exceedingly difficult for systems with non-negligible contributions from multiple scattering. Already small contributions of multiple scattering can result in large analysis errors. Particularly for larger particles with high scattering contrast, this limits the technique to very low particle concentrations. A large variety of systems are therefore excluded from investigations with conventional dynamic light scattering. However, it is possible to suppress multiple scattering in DLS via the cross-correlation approach. The general idea is to isolate singly scattered light and suppress undesired contributions from multiple scattering in a DLS experiment. Different implementations of cross-correlation light scattering have been developed and applied. Currently, the most successful scheme is the so-called 3D cross-correlation method. The same method can also be used to correct Static Light Scattering (SLS) data for multiple scattering contributions. Alternatively, in the limit of strong multiple scattering, a variant of dynamic light scattering called Diffusing Wave Spectroscopy (DWS) can be applied.
Data Analysis
There are three main methods to analyze DLS Data: CUMULANT, CONTIN, and CORENN.
The CUMULANT technique is the most robust technique if data is noisy, but it can only determine a mean particle size and if Gaussian distribution around this mean size is assumed, it can determine the width of this distribution. This is often referred to as the Polydispersity Index (PDI).
CONTIN1,2,3 used to be the best choice if a bi-modal particle distribution is present in the sample. CONTIN however is very sensitive to any noise present in the data. Often the only way to obtain reliable results is by making additional assumptions. This however means that there different versions of CONTIN. Often the specific assumptions are not mentioned. Typically the assumption of a Gaussian distribution for the individual particle populations is required. But other more severe restrictions are frequently applied. Due to the limitation of CONTIN, it has been replaced by CORENN, which is more suited for multi-modal particle size distributions.
CORENN is an algorithm that was developed by LSI. It is based on a constrain weighted, regularized non-linear, least-squares fit with free baseline for integral inversion of the ill posed problem. It is a robust technique that provides reliable results even in the presence of data noise. Unlike CONTIN is does not require additional restrictions or assumptions.
[1] S.W. Provencher: Inverse problems in polymer characterization: Direct analysis of polydispersity with photon correlation spectroscopy. Makromol. Chem. 180, 201 (1979).
[2] S.W. Provencher: A constrained regularization method for inverting data represented by linear algebraic or integral equations. Comput. Phys. Commun. 27, 213 (1982).
[3] S.W. Provencher: CONTIN: A general purpose constrained regularization program for inverting noisy linear algebraic and integral equations. Comput. Phys. Commun. 27, 229 (1982)
